01/01/25 - #softwareengineering #pyhton #avltree

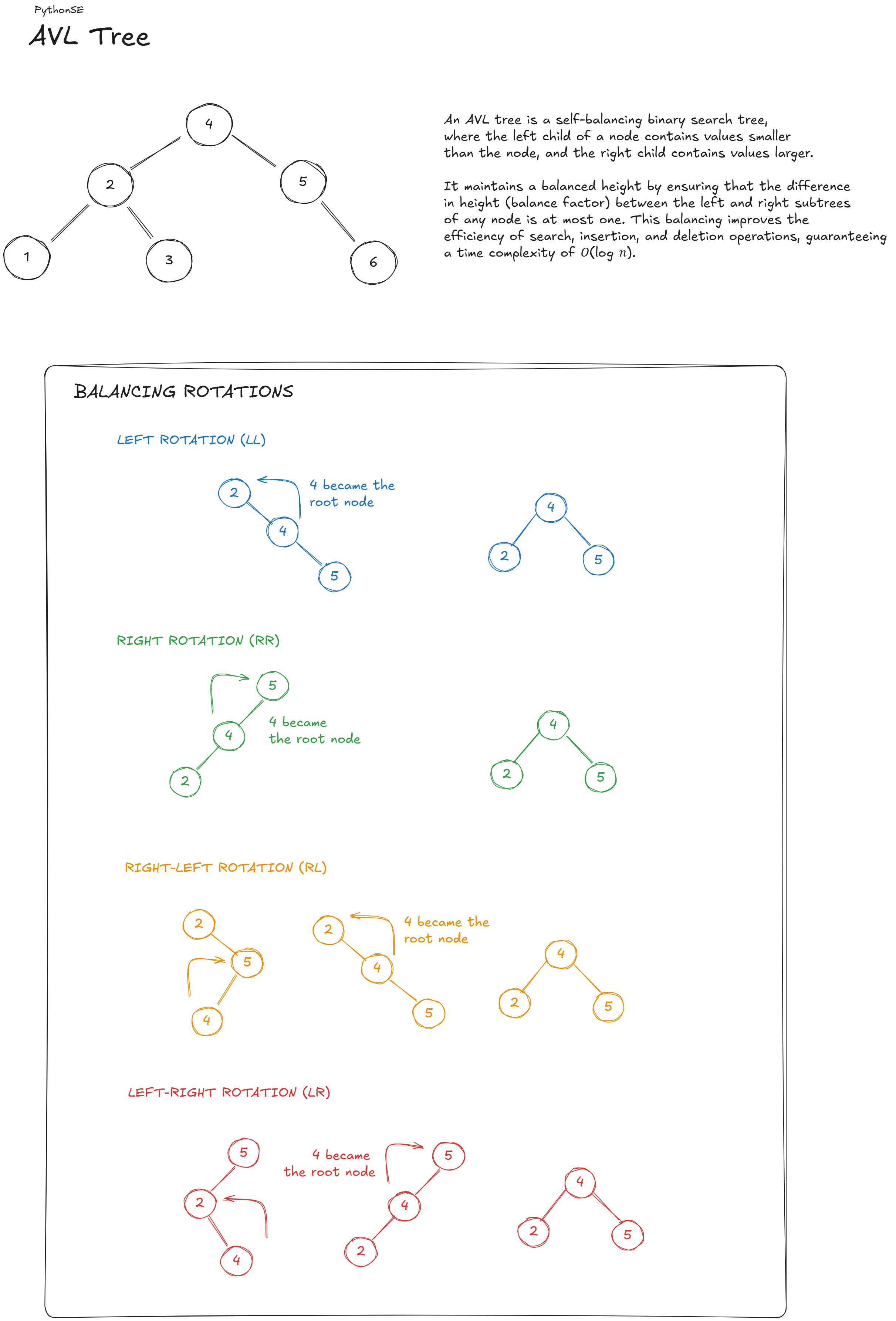
The AVL Tree (named after its inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. Its core feature is that the difference in height between the left and right subtrees of any node (called the balance factor) is at most 1. This balance guarantees logarithmic time complexity for operations such as insertion, deletion, and lookup, making it a powerful tool for applications requiring efficient sorted data access.

To grasp the AVL tree intuitively, let’s visualize its balancing process:

• Insertion: When a new node is added, the balance factor of affected nodes is recalculated. If a node becomes unbalanced (balance factor is less than -1 or greater than 1), rotations (single or double) are applied to restore balance.

• Rotations:

  • Right Rotation (RR): When the left subtree is too tall, the right rotation shifts nodes rightward.
  • Left Rotation (LL): When the right subtree is too tall, the left rotation shifts nodes leftward.
  • Left-Right (LR) and Right-Left (RL): These occur when the tree requires two rotations to resolve imbalance.

Implementation

Here is a basic implementation of an AVL Tree in Python. You can also find this code on Python SE GitHub repository.

class Node:
    def __init__(self, key):
        """
        Node structure for AVL Tree.
        Each node contains:
        - key: The value of the node
        - left: Reference to the left child (initially None)
        - right: Reference to the right child (initially None)
        - height: Height of the node (default is 1 for new nodes)
        """
        self.key = key
        self.left = None
        self.right = None
        self.height = 1  # Height is important for balancing the AVL Tree

class AVLTree:
    def get_height(self, node):
        """
        Returns the height of a given node.
        If the node is None, height is 0.
        """
        return node.height if node else 0

    def get_balance(self, node):
        """
        Calculates and returns the balance factor of a node.
        Balance factor = height of left subtree - height of right subtree.
        """
        return self.get_height(node.left) - self.get_height(node.right)

    def rotate_right(self, y):
        """
        Performs a right rotation on the subtree rooted at node y.
        Returns the new root of the rotated subtree.
        """
        x = y.left  # x becomes the new root
        T2 = x.right  # T2 is the subtree that will be moved

        # Perform rotation
        x.right = y
        y.left = T2

        # Update heights after rotation
        y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))
        x.height = 1 + max(self.get_height(x.left), self.get_height(x.right))

        return x  # New root after rotation

    def rotate_left(self, x):
        """
        Performs a left rotation on the subtree rooted at node x.
        Returns the new root of the rotated subtree.
        """
        y = x.right  # y becomes the new root
        T2 = y.left  # T2 is the subtree that will be moved

        # Perform rotation
        y.left = x
        x.right = T2

        # Update heights after rotation
        x.height = 1 + max(self.get_height(x.left), self.get_height(x.right))
        y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))

        return y  # New root after rotation

    def insert(self, root, key):
        """
        Inserts a new key into the AVL Tree rooted at 'root'.
        Balances the tree after insertion if necessary.
        """
        # Step 1: Perform standard BST insertion
        if not root:  # If the tree is empty, create a new node
            return Node(key)
        if key < root.key:
            # Insert in the left subtree if the key is smaller
            root.left = self.insert(root.left, key)
        else:
            # Insert in the right subtree if the key is larger
            root.right = self.insert(root.right, key)

        # Step 2: Update height of the current node
        root.height = 1 + max(self.get_height(root.left), self.get_height(root.right))

        # Step 3: Calculate the balance factor of the current node
        balance = self.get_balance(root)

        # Step 4: Check for imbalance and perform rotations if needed

        # Left Left Case (unbalanced due to left-heavy subtree)
        if balance > 1 and key < root.left.key:
            return self.rotate_right(root)

        # Right Right Case (unbalanced due to right-heavy subtree)
        if balance < -1 and key > root.right.key:
            return self.rotate_left(root)

        # Left Right Case (left subtree is heavy, but imbalance is caused by right child of left subtree)
        if balance > 1 and key > root.left.key:
            root.left = self.rotate_left(root.left)  # First rotate left
            return self.rotate_right(root)  # Then rotate right

        # Right Left Case (right subtree is heavy, but imbalance is caused by left child of right subtree)
        if balance < -1 and key < root.right.key:
            root.right = self.rotate_right(root.right)  # First rotate right
            return self.rotate_left(root)  # Then rotate left

        return root  # Return the unchanged root if no rotation is needed


# Example usage #
tree = AVLTree()
root = None

# Insert elements into the AVL Tree
elements = [10, 20, 30, 40, 50, 25]
for elem in elements:
    root = tree.insert(root, elem)